Funzione gradino di Heaviside

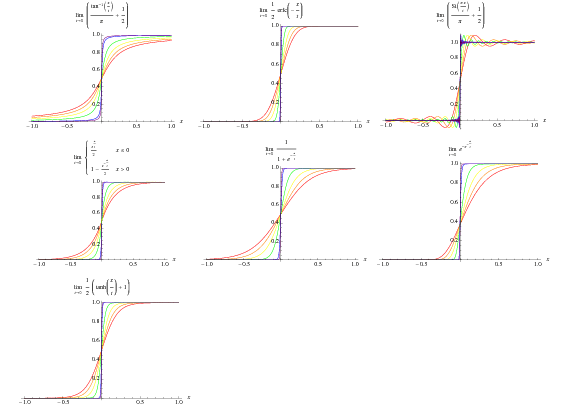
In matematica e fisica, la funzione gradino di Heaviside o funzione a gradino unitaria, il cui nome si deve a Oliver Heaviside, è una funzione discontinua che ha valore zero per argomenti negativi e uno per argomenti positivi. Può essere definita sia come una funzione continua a tratti o come una distribuzione.

La derivata distribuzionale della funzione di Heaviside ${\displaystyle H}$ è la delta di Dirac ${\displaystyle \delta (x)}$:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}H(x)=\delta (x),}$

mentre la funzione rampa ${\displaystyle R}$ ne è la primitiva:

${\displaystyle R(x):=\int _{-\infty }^{x}H(\xi )\mathop {} \!\mathrm {d} \xi =xH(x).}$

La funzione a gradino è usata nella matematica della teoria del controllo e nell'elaborazione dei segnali per rappresentare un segnale che si attiva a partire da un tempo specificato e rimane attivo indefinitamente.

Inoltre tale funzione è utilizzata in fluidodinamica per lo studio di flussi multifase con interfaccia sharp.

Definizione

Si indica con:

${\displaystyle \Theta (x)={\begin{cases}0,&x<0\\1,&x\geqslant 0.\end{cases}}}$

Spesso, al posto di ${\displaystyle \Theta (x)}$, si usano le notazioni ${\displaystyle \delta ^{(-1)}(x)}$, ${\displaystyle u(x)}$ o ${\displaystyle h(x)}$, o ancora, con abuso di notazione, ${\displaystyle 1(x)}$.

Se viene definita come una distribuzione, è la funzione ${\displaystyle \Theta (x)}$ tale per cui:

${\displaystyle \int \Theta (x)f'(x)\mathop {} \!\mathrm {d} x=-f(0),}$

dove ${\displaystyle f'}$è la derivata di una funzione sufficientemente liscia che decresce all'infinito con andamento sufficientemente rapido.

Una rappresentazione integrale della funzione gradino è la seguente:

${\displaystyle \Theta (x)=\lim _{\varepsilon \to 0}\left(-{1 \over 2\pi i}\int _{-\infty }^{\infty }{1 \over \tau i\varepsilon }e^{-ix\tau }\mathop {} \!\mathrm {d} \tau \right).}$

Si tratta della funzione di ripartizione di una variabile casuale che è quasi sicuramente 0 (vedi variabile casuale degenere).

La funzione di Heaviside è l'integrale della delta di Dirac:

${\displaystyle \Theta (x)=\int _{-\infty }^{x}{\delta (t)}\mathop {} \!\mathrm {d} t.}$

Il valore di ${\displaystyle \Theta (0)}$ non è del tutto standard: alcuni scrittori assumono ${\displaystyle \Theta (0)=0}$, altri ${\displaystyle \Theta (0)=1.}$ La scelta più utilizzata rimane comunque ${\displaystyle \Theta (0)=1/2}$ perché permette di ridefinire la funzione di Heaviside attraverso la funzione segno. Questo ne dà una definizione più generale:

${\displaystyle \Theta (x)={\frac {1}{2}}\left(1 \operatorname {sgn} x\right)={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}}$

Per rimuovere l'ambiguità sul valore di ${\displaystyle \Theta (0)}$ da utilizzare, si può scrivere un pedice che lo specifica:

${\displaystyle \Theta _{n}(x)={\begin{cases}0,&x<0\\n,&x=0\\1,&x>0.\end{cases}}}$

Tuttavia la stessa notazione è usata per indicare un gradino ritardato:

${\displaystyle \Theta _{T}(t)=\Theta (t-T).}$

Il prodotto di una funzione per la funzione ${\displaystyle \Theta }$ dà una funzione unilatera.

Forma discreta

Si può anche definire una forma alternativa del gradino unitario come funzione di una variabile discreta ${\displaystyle n}$:

${\displaystyle \Theta [n]={\begin{cases}0,&n<0\\1,&n\geq 0,\end{cases}}}$

dove ${\displaystyle n}$ è intera. Questa funzione è la somma fino a ${\displaystyle n}$ della delta di Kronecker:

${\displaystyle \Theta [n]=\sum _{k=-\infty }^{n}\delta [k],}$

dove ${\displaystyle \delta [k]=\delta _{k,0}}$ è la delta di Dirac.

Trasformata di Fourier

Un altro modo per scrivere il gradino di Heaviside è

${\displaystyle \Theta (t)=\lim _{\alpha \to 0}\exp(-t\alpha ^{|t|/t})}$

la cui trasformata di Fourier è:

${\displaystyle {\tilde {\Theta }}(t)={\frac {1}{i\omega }} \pi \delta (\omega ),}$

dove ${\displaystyle \delta (\omega )}$è la delta di Dirac. Cioè lo spettro in frequenza del gradino di Heaviside è ${\displaystyle 1/(i\omega )}$ eccetto che in ${\displaystyle \omega =0}$, dove è presente una singolarità in cui è concentrato lo spettro.

Bibliografia

• Milton Abramowitz e Irene Stegun, Handbook of mathematical functions: with formulas, graphs, and mathematical tables, collana Dover books on mathematics, 9. Dover print.; [Nachdr. der Ausg. von 1972], Dover Publ, 2013, ISBN 978-0-486-61272-0.
• (EN) Bracewell, R. "Heaviside's Unit Step Function, H(x)." The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 61-65, 2000.
• (EN) Ram P. Kanwal, Distributional Derivatives of Functions with Jump Discontinuities, Birkhäuser, 1998, pp. 99-137, DOI:10.1007/978-1-4684-0035-9_5, ISBN 978-1-4684-0035-9. URL consultato il 30 giugno 2023.
• (EN) Spanier, J. and Oldham, K. B. "The Unit-Step u(x-a) and Related Functions." Ch. 8 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 63-69, 1987.

Voci correlate

• Delta di Dirac
• Funzione gradino
• Funzione rettangolo
• Funzione segno

Altri progetti

• Wikimedia Commons contiene immagini o altri file su funzione gradino di Heaviside

Collegamenti esterni

• (EN) Eric W. Weisstein, Heaviside Step Function, su MathWorld, Wolfram Research.